Trig - intro to basic ratios

The field of Trigonometry grew from the interest held by the ancient Arabs and Greeks in astronomy. In tracing the movement of the stars and measuring the rotation of Earth, they were constantly examining circles and the angles within them.

Hipparchus is widely regarded as the founder of Trigonometry.

He was born in 190 BC in Nicaea, Bithynia (in present day Turkey) and he died in 120 BC on the island of Rhodes, Greece.

He was a mathematician of great ability and great insight.
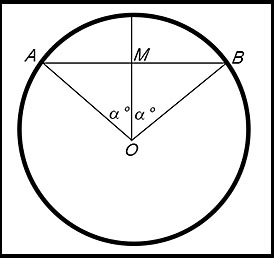For example, in his work with the circle, he proposed that he should divide the shape into 360° so that it could be analysed in more depth. This led him into also suggesting that locations on the sphere of Earth could be defined using latitude and longitude references.

Amongst the many problems in which Hipparchus was interested was that of determining the length of a chord in a circle. He understood that the length AB - which was twice the length AM - was dependent on the size of the angle α at the cengtre of the circle.

So he developed a table of values for the length of half a chord based on the unit circle - where the radius was 1 - for all values of α from 0.5° to 90°. To determine lengths of chords for circles of radius other than 1, the value in Hipparchus' table for the given angle could be simply multiplied by the value of the radius.

As we will see later, the Table developed by Hipparchus was really giving the values for sin α°. At this stage however, the focus was on chord length and not on the angle.

The way the ratio documented in Hipparchus' table was calculated (AM÷AO) was later called the SINE of an angle. This ratio is actually a roundabout way but it is based directly on the approach developed by Hipparchus.

The identification of the trigonometric ratios.

About 1,000 years later, the emphasis began to change to focus more on the sides of a triangle in relation to the angle. This change was led by some of the great Hindu mathematicians. The names of the ratios reflected their geometrical interpretations - and it is still the easiest way to remember them.

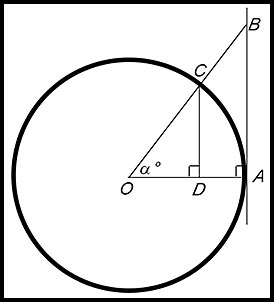We start with a circle with centre at O.
A tangent is drawn at any point - say A - and a line is drawn to link A to the centre O - which is of course the radius.

The properties of a circle remind us that the angle OAB is a right angle (= 90°).

Remember that a line segment is the name given to that part of a line defined by two distinct end points. Hence when we mark a point B at any point along the tangent, AB can be referred to as a line segment. In this case it is also a tangent segment (for obvious reasons).

Also remember that a secant is any line which cuts a circle at two distinct points. Hence the line from B to O (and extended) is a secant and so BO can be described as a secant segment.

Adopting the ideas of Hipparchus, we can see that the larger the angle α° becomes (and so B moves further upwards):

the longer the tangent segment AB becomes;
the longer the secant segment BO becomes.

So the ratio of AB to AO measures how big the angle α° is.

Expressing angles as ratios.

To report the ratio for the tangent segment, we can write .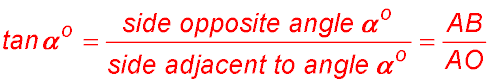

We use the word "tan" as being short for tangent - which might be the length we are here trying to calculate.

If we used the secant segment OB - which is the hypotenuse - we could write the ratio of OB to OA (again using the radius as the standard of the measurement).

So - where of course sec is short for secant.

As is shown in the video related to this page, we can use these two ratios to calculate either of the segment lengths used in these ratios - or the size of the angle α°.

But wait - there is more!!!!

Ratios for the complementary angles.

We now determine the values related to the complementary angle of α° for each of the two ratios in the right angle triangle. We use the same definition of the ratio used above.

So referencing the complementary angle OBA and using the definitions of the sides to consider from the above:

which we now refer to as cot α° (complementary tan).

The last ratios.

The other possible combination of sides in the triangle is that used by Hipparchus to measure the lengths of chords - the ratio of half the chord divided by the radius of the circle.

The first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy was Aryabhata.

He lived about 650 years after Hipparchus.

Aryabhata used the ratio in the Sanskrit form meaning "half chord". This term was translated into various forms in different languages until finally it was translated into Latin from Arabic as sinus. We then modified that at some time to become sine (often written as sin).

In the diagram of the circle above, CD and BA are parallel - so triangles OCD and OBA are similar. With this view, we recognise the segment CD as being half a chord of the circle - and so we are again adopting Hipparchus' view for the ratio.

Hence .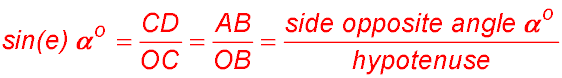

Also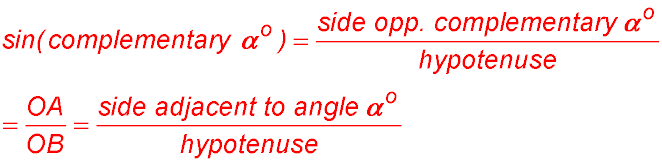

which is referred to as cosine α° (complementary sine).

Similarly,

which we now refer to as cosec α° (complementary sec).

Summary

In our texts, we tend to change the order of the six ratios - but also forget the links to the meanings. Order in writing the ratios is irrelevant but remember the connections for each ratio so that you can easily and correctly identify which ratio is required to solve a given problem.

Hope the following table helps.

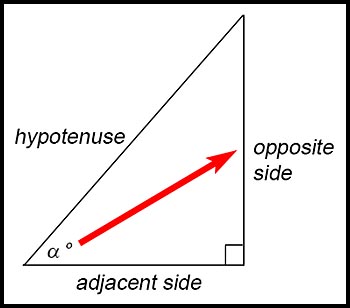
It is a good strategy
to draw an arrow from the given angle in the triangle
to the opposite side
before you start identifying the required ratio.


Ratio	Ratio for the complementary angle (or the reciprocal)

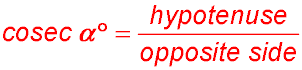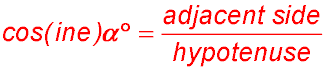Now have a look at the video.